Il existe une autre manière de voir les choses de cet univers en ne se fondant pas sur la matière mais sur la structure géométrique de ces choses. Cela constitue une tradition qui s'est perpétuée à travers les siècles, et que l'on recommence à connaître aujourd'hui grâce à des travaux scientifiques. Par exemple, Nassim Haramein, physicien autodidacte, nous fait part d'une des ces réalités que l'on recommence à comprendre aujourd'hui. Et c'est à partir d'une idée fort simple. Cette idée, c'est que tout simplement, la géométrie de l'espace est aussi importante que l'étude de la matière. Selon lui, nous pourions compléter la recherche en physique des particules par une autre recherche : celle des géométries et des structures de division du vide qui génèrent ces particules.

Qu'est-ce à dire ?

Cela signifie, par exemple, que pour un amas de galaxies, il y a une structure de division du vide qui y correspond. Pour un nuage d'electrons, une division de l'espace vide y correspond aussi. Pour les particules subatomiques (mesons, baryons) aussi, il existe une division de l'espace vide particulière. Etc. Chaque chose dispose en somme d'une géométrie du vide qui lui donne raison, qui lui permet d'exister.

En d'autres termes, il existe pour toute particule une géométrie qui structure le vide et fait advenir cette particule. Quelles sont les principales géométries dont il est question ici?

D'abord, l'octahèdre cubique :

Cette forme compliquée permet un équilibre parfait : c'est le "vector equilibrium" tel que décrit par le célèbre géomètre Buckminster Fuller. Il se retrouve dans la disposition des mesons, des particules subatomiques.

Mais sans aller chercher aussi loin, nous avons les quarks qui constituent le proton et qui sont disposés selon une forme triangulaire, toute simple :

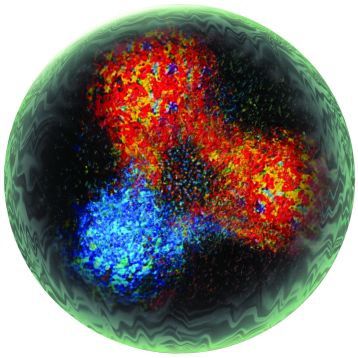
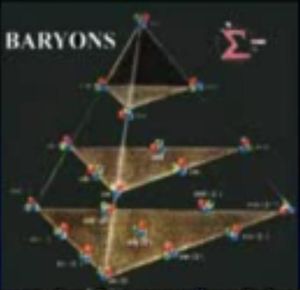
Lorsqu'on passe dans la 3D, le triangle devient un tétrahèdre et on obtient la disposition des baryons :

Mais on trouve des formes plus complexes comme celles prises par les nuages électroniques de certains atomes :

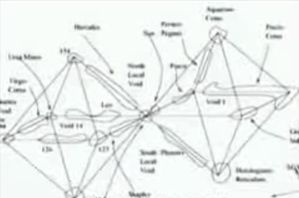
Mais il n'y a pas que les particules qui ont des géométries intéressantes : les amas de galaxies aussi, et ils sont disposés selon des structures de doubles pyramides inversées appelées octaèdres :

Est-ce à dire que tout est organisé à partir d'une géométrie dans l'univers ? De plus amples explications seront nécessaires pour le prouver.